1999年02月01日《数学游戏的胜利之道》第24章节第735页有记载索玛立方的介绍以及索玛立方的240个解法。
该书的ISBN号为0-12-091102-7。

索玛立方,英文叫SOMA,它的设计师是Piet Hein。
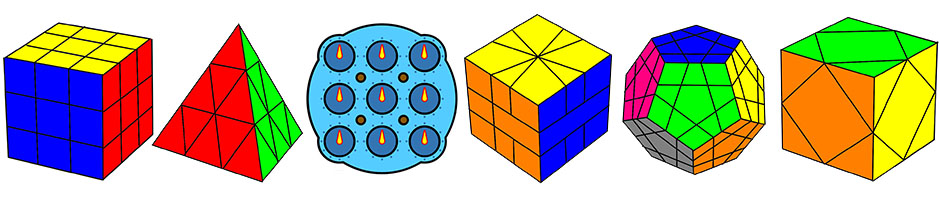
四块1 x 1 x 1的立方体黏成了6种非凸形状积木。
三块1 x 1 x 1的立方体黏成了1种非凸形状积木。
4 x 6 + 3 x 1 = 27
Piet Hein的难题就是将他们拼成一个3 x 3 x 3的立方体。
很多人在十分钟之内就解决了这个难题,所以觉得这不会很难。
但其实这只是一种解法,要找到全部非常困难,不会使用计算机的人一直无法找到他所有的解法。
我们建议将各种积木处理成不同的颜色,这样就可以合理地写出解法。
1号块白色、White、使用W表示。
2号块黄色、Yellow、使用Y表示。
3号块绿色、Green、使用G表示。
4号块橙色、Orange、使用O表示。
5号块蓝色、Blue、使用L表示(这里避免与黑色混淆,使用L字母)。
6号块红色、Red、使用R表示。
7号块黑色、Black、使用B表示。
隐藏在索玛里的秘密
拼索玛必须满足一些隐藏的约束以及显而易见的约束。
这给大多数人造成了更多的麻烦。
3 x 3 x 3的立方体
有8个顶点单元(vertex cells)
有12个棱单元(edge cells)
有6个面单元(face cells)
有1个中央单元(central cells)
我们看一个每一个块最多可以占据几个顶点单元:
W,1.
Y,2.
G,2.
O,1.
L,1.
R,1.
B,1.
又由于内部凹陷一块,顶点上就会少一块。所以绿色的那块的脊柱只可以沿着边缘。
接下来,我们对3 x 3 x 3的立方体的每一个块进行交替上色。
让相同的颜色的块不相连。
8个顶点单元和6个面单元,涂成14个火焰色。
12个棱单元和1个中央单元,涂成13个祖母绿色。
然后我们已知的一个解法中,每一个块占据了:

除去黄色、橙色、蓝色、红色以及我们了解的绿色,在每一个解法中必须占据这些数字。
因此白色和黑色必须如此,这两个颜色中一块或两块互换,都会改变总数。白色必须有2个火焰色1个祖母绿,黑色必须1个火焰色3个祖母绿。
我们将每一块积木放进3 x 3 x 3的立方体,如下面的图:
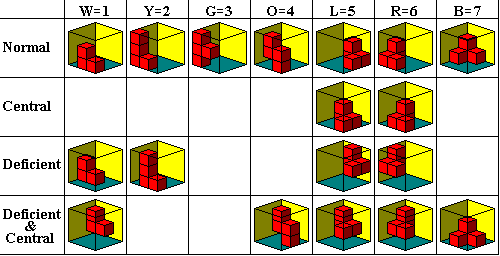
你会看到,知道立方体旋转为止,任何一块的放置位置都取决于它是否陷入(deficient)以及是否占据了中心(central)。
SOMA的一个隐藏的秘密是你可能一开始就放错了一块,
当你花费大量时间组装更多的块之前,这样的错误就会显出效果了,
你会花很多时间,却怎么搭也搭不好。
例如,如果你将白色小块的一角放入立方体的一角,就会发生这种情况。
但是,如果仅将一块放置在允许的位置,则几乎在开始时就会找到解决方案。